Hausaufgabenseite Hallo liebe Schüler. Zu jeder Unterrichtsstunde bekomme ich von euch viel Post und teilweise sehr sehr schöne Darstellungen oder Lösungsideen. Vielen Dank dafür. Damit möglichst viele von euch davon profitieren können, sollen diese Lösungen hier vorgestellt werden. Zu Lektion 1: Aufgabe 1: Übersetze ins Muggelsystem: SNAPE (Za)= QGLJ (Za)= ZZZZZ (Za)= Aufgabe 2: Übersetze ins Zaubersystem: 1018717295 (Mu) = Cecilia aus Gryffindor schickte mir dazu diese Lösung, die formal sehr übersichtlich dargestellt ist: Hausaufgabe 1) S = 2 8 * 3 6 * 3 6 * 3 6 * 3 6 = 4 7 0 2 9 2 4 8 N = 2 3 * 3 6 * 3 6 * 3 6 = 1 0 7 3 0 8 8 A = 1 0 * 3 6 * 3 6 = 1 2 9 6 0 P = 2 5 * 3 6 = 9 0 0 E = 1 4 = 1 4 4 8 1 1 6 2 1 0 Q = 2 6 * 3 6 * 3 6 * 3 6 = 1 2 1 3 0 5 6 G = 1 6 * 3 6 * 3 6 = 2 0 7 3 6 L = 2 1 * 3 6 = 7 5 6 J = 1 9 = 1 9 1 2 3 4 5 6 7 Z = 3 5 * 3 6 * 3 6 * 3 6 * 3 6 = 5 8 7 8 6 5 6 0 Z = 3 5 * 3 6 * 3 6 * 3 6 = 1 6 3 2 9 6 0 Z = 3 5 * 3 6 * 3 6 = 4 5 3 6 0 Z = 3 5 * 3 6 = 1 2 6 0 Z = 3 5 = 3 5 6 0 4 6 6 1 7 5 Hausaufgabe 2) 1 0 1 8 7 1 7 2 9 5 : 3 6 = 2 8 2 9 7 7 0 2 7 2 2 9 8 2 8 2 9 7 7 0 2 : 3 6 = 7 8 6 0 4 7 2 8 8 2 5 2 1 0 7 3 0 9 7 8 6 0 4 7 : 3 6 = 2 1 8 3 4 7 2 2 8 8 7 2 3 5 1 2 1 7 6 6 2 1 8 3 4 : 3 6 = 6 0 6 3 2 4 2 1 6 3 6 2 1 6 2 7 7 1 7 3 0 0 2 3 6 0 6 : 3 6 = 1 6 2 5 2 0 2 8 8 0 3 6 2 5 2 1 7 0 1 2 4 2 3 4 2 4 6 2 5 2 1 4 4 1 0 8 2 1 6 2 1 6 0 9 2 6 2 1 6 7 1 8 3 0 0 2 5 2 1 4 4 9 5 1 0 2 3 7 2 2 3 1 6 = G 3 0 = U L ö s u n g = G u i n a n 1 8 = I 2 3 = N 1 0 = A 2 3 = N Bei den Hausaufgaben von Heir aus Slytherin gefiel mir besonders, dass er außer den Rechnungen im Muggelsystem in der ersten Zeile auch noch die Rechnung im Zaubersystem mit übernommen hat: 1.) Snape =S*104+N*103+A*102+P*10+E (alles Za) =28*364+23*363+10*362+25*36+14 (alles Mu) =47029248+1073088+12960+900+14 (alles Mu) =48116210 2.) QGLJ =Q*103+G*102+L*10+J (alles Za) =26*363+16*362+21*36+19 (alles Mu) =1213056+20736+756+19 (alles Mu) =1234567 3.) ZZZZZ =Z*(104+103+102+10+1) (alles Za) =35*(364+363+362+36+1) (alles Mu) =35*(1727605) (alles Mu) =60466175   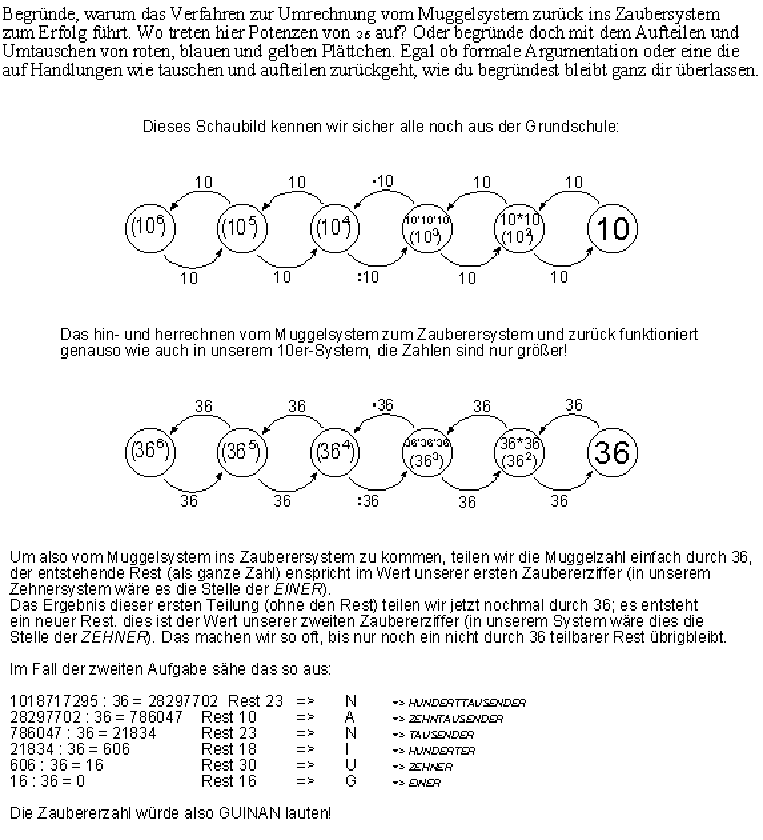2. Übersetze ins Zaubersystem: 1018717295 (Mu) = GUINAN (Za) Rechnung: 1018717295/36=28297702 Rest 23 23 (Mu)=N (Za) 28297702/36=786047 Rest 10 10 (Mu)=A (Za) 786047/36=21834 Rest 23 23 (Mu)=N (Za) 21834/36=606 Rest 18 18 (Mu)=I (Za) 606/36=16 Rest 30 30 (Mu)=U (Za) 16/36=0 Rest 16 16 (Mu)=G (Za) Bei Aufgabe 1 c) habe ich noch eine schöne Idee von WallaceW aus ???? erhalten. Allerdings ist seine Darstellung nicht ganz korrekt, denn ZZZZZ ist NICHT dasselbe wie ZZZZZ+1! Die Idee lässt sich aber sehr leicht retten und vereinfacht dann die Aufgabe sehr! Prima Wallace! Er schrieb: ZZZZZ=ZZZZZ+1=100000=60466176-1=60466175 Also das Gleichheitszeichen darf hier nicht verwendet werden, schreib das doch einfach in verschiedene Zeilen, etwa so: ZZZZZ=? ZZZZZ+1=100000=60466176 ZZZZZ=60466176-1=60466175 Jetzt kommt die Begründungsaufgabe. Leider habe ich sie versehendlich falsch gestellt, denn viel mehr als eine Begründung der Umrechnung vom Zauber- ins Muggelsystem interessierte mich die Begründung für den umgekehrten Weg, für die Umrechnung vom Muggel- ins Zaubersystem. Da ich aber zu beiden Richtungen Begründungen geschickt bekommen habe, hat dieser kleine Fehler meinerseits nun den Vorteil, dass ich euch beide Richtungen anbieten kann. Zuerst zur Ursprungsaufgabe: Aufgabe3: Begründe, warum das Verfahren zur Umrechnung vom Zaubersystem zurück ins Muggelsystem zum Erfolg führt. Wo treten hier Potenzen von 36 auf? Oder begründe doch mit dem Aufteilen und Umtauschen von roten, blauen und gelben Plättchen. Egal ob formale Argumentation oder eine die auf Handlungen wie tauschen und aufteilen zurückgeht, wie du begründest bleibt ganz dir überlassen. Zuerst stelle ich euch eine sehr formale Argumentation von Fleurette Calice aus Ravenclaw vor: 3. Das Zaubersystem hat im Gegensatz zum Muggelsystem nicht die Zahl 10 als Grundlage sondern 36. Das beruht darauf, dass es im Muggelsystem 10 verschiedene Ziffern gibt ( 0-9), im Zaubersystem dagegen 36 (0-Z). Nach 36 Zahlen, die man nur mit je einer Ziffer darstellen kann wie z.B. 2, F, Y, geht man zur 2. Stelle über und beginnt dort wieder von 1 bis zu Z. Je größer die Zahl, desto mehr Stellen hat sie, egal ob im Muggel- oder Zaubersystem. Will man nun eine Zahl aus dem Zauber- in das Muggelsystem übersetzten, muss man nicht nur die einzelnen Ziffern übersetzten wie z.B. A(za) = 10 (mu), sondern auch die Stelle beachten. Je nach STelle wird die übersetzte Ziffer mit einer 36er-Potenzmultipliziert., da 36 wie gesagt die Grundlage des Systems bildet. So wird die hinterste Stelle mit 36 hoch 0 = 1, die nächste mit 36 hoch 1 = 36, die nächste mit 36 hoch 2 = 1296 usw. multipliziert. Die Summe dieser einzelnen mit einer 36er-Potenz mutiplizierten Ziffern ergibt dann die Zahl im Muggelsystem.   Bei der Begründung von Zareeja aus Gryffindor hat mir gut gefallen, dass sie uns noch einmal daran erinnert, dass das alles gar nicht so schwer ist, weil das 10er-System, das wir in der Schule alle gelernt haben, genau so funktioniert. Sie schreibt: Im Muggelsystem sind die Stellenwerte folgendermaßen: Ganz rechts sind die 1er, links daneben die 10er, wieder daneben die 100er... usw. (Das lernt man in Muggelschulen schon in der 1. oder 2. Klasse.) Im Zaubersystem ist es genauso: Ganz rechts die 1er, daneben die 10er (Za), wieder daneben die 100er (auch Za)... 10 (Za) = 36 (Mu) 100 (Za) = 1296 (Mu) = 36² (Mu) (Hier tritt schon die erste 36er-Potenz auf.)     Als Beispiel nehmen wir mal die Zahl: BEISPIEL Das L gibt die 1er an, im Muggelsystem hieße das, es sind 21 1er. (bzw. 20 10er (Mu) und 1 1er (Mu)) Das E sind die 10er, im Muggelsystem also 14 36er. Das I sind 100er, im Muggelsystem 18 1296er, oder 18 36²er Das P sind 1000er, im Muggelsystem 25 46656er, oder 25 36³er. (Auch 36er-Potenzen) etc. Wenn wir also im Zaubersystem "I*100" bzw. "I*10²" schreiben, ist das das gleiche, wie im Muggelsystem "18*1296" bzw. "18*36²". Deswegen funktioniert diese Art des Umrechnens. Lawynia aus Gryffindor übernimmt die Idee mit den Legos für ihre Argumentation: 3.) Wenn man Snape (z.B.) mit den verschiedenen Potezen multipliziert kommt man auf das richtige Ergebnis. Also: 28 (für s) * 36^4 + 23 (n) * 36^3 + 10 (a) *36^2 + 25 (p) *36 + 14 (e) man kann auch sagen: Man hat also 28 weise Legos (s), 23 schwarze Legos (n), 10 gelbe (a), 25 blaue (p) und 14 rote (e). Nun will amn aber nur rote legos haben (da alle roten Legos genau das selbe sind wie Anape im Zaubersystem). Damit alles am Ende rote Legos sind rechnet man: 28 *36 ^4. Nun hat man (0 weise Legos) 23 schwarze, 10 gelbe, 25 blaue und insgesamt 47029262 rote. Nun die schwarzen in rot! 23*36^3. Nun hat man (0 weise Legos, 0 schwarze), 10 gelbe, 25 blaue und insgesamt 48102350 rote Legos! Nun die gelben in rot!!! 10*36^2. Man hat nun (0 weise, 0 schwarze, 0 gelbe), 25 blaue und insgesamt 48115310 rote Legos. Zuletzt noch die blauen in rot! 25*36. Man hat nun nur noch rote! Insgesamt 48116210. Ich hoffe man kann meine Erklärung verstehen!!!! Mit Kruemel aus Ravenclaw habe ich wohl einen Schüler, der schon etwas weiter ist, er macht sich zum Beispiel auch schon Gedanken über Systembrüche und darüber, ob diese Verfahren auch in anderen Systemen funktionieren. Seine Argumentation ist von allen die formalste. Aber es gibt immer Schüler, die in einer formalen Argumentation mehr Klarheiten finden als in einer auf Handlungen ausgerichteten, daher soll euch seine Argumentation auch nicht vorenthalten werden:   Beim Schreiben einer mehrstelligen Zahl steht jede Stelle der Zahl für die häufigkeit einer bestimmten Potenz. Der Wert dieser Potenz hängt von der Position der Ziffer und der Art des Systems ab. Die Art des Systems bestimmt die Basis der Potenz im Zaubersystem gibt es (incluseiver der 0 (NULL)) 36 verschiedene Ziffern. Die Basis der Potenz beträgt somit 36 Die Stelle der Ziffer gibt den Exponenten der Potenz an. Die Stelle direkt vor dem Komma hat den Exponenten 0. Bei jeder weiteren Stelle vor dem Komma erhöht sich der Exponent um 1 bei jeder Stelle hinter dem Komma erniedrigt sich der Exponent um 1. Ein Beispiel dazu : G = 16 * 36^0 = 16 * 1 = 16 G0 = 16 * 36^1 = 16 * 36 = 576 _ 0,G = 16 * 36^-1 = 16 * (1/36) = 16 /36 = 4/9 = 0.4 (genau hier taucht die Idee mit den Systembrüchen auf (Anm. von Epsilona)) Auf diese Weise funktioniert die Umrechnung von einem System in das Dezimal- (oder Muggel-) System. Diese Methode funktioniert allerdings aus jedem anderen System auf die gleiche Weise. Potenzen treten bei der Stellenweisen umrechnung auf und werden durch die Art der Ursprungssystems bestimmt.     Den Umgekehrten Fall, die Umrechnung vom Muggel- ins Zaubersystem, hat uns wieder Heir of Slytherin gut begründet:   Diese Methode führt zum Erfolg, da sowohl die Muggelzahl als auch die Zaubererzahl auf dem selben Prinzip, dem Bündeln von Zahlen (rote Plättchen werden zu blauen gebündelt, die blauen zu gelben usw.), beruhen. Für die Umwandlung stellt man zuerst den ungebündelten Zustand her. In unserer Aufgabe bedeutet dies, statt 5 roten Plättchen, 9 blauen, 2 gelben, 7 schwarzen ... 1018717295 rote Plättchen zu verwenden. Jetzt ist die 10er-Bündelung des Muggelsystems aufgehoben. Da das Zahlensystem der Zauberer auf 36er-Bündelungen beruht, müssen die 1018717295 roten Plättchen jetzt entsprechend gebündelt werden. Hierfür legt man sie in Gruppen zu je 36 Plättchen zusammen. In unserem Beispiel ergibt das 28297702 Gruppen, die jetzt gegen jeweils ein blaues Plättchen eingetauscht werden. Die übrig gebliebenen 23 roten Plättchen bleiben an ihrem Platz und bilden die letzte „Ziffer" der Zahl im Zauberersystem, ein „N". Die 28297702 blauen Plättchen werden jetzt wieder zu 36er-Gruppen zusammengelegt. In diesem Fall werden 786047 36er-Gruppen gebildet, welche gegen je ein gelbes Plättchen ausgetauscht werden. Die verbliebenen Plättchen (hier: 10 Stck.) bilden die vorletzte „Ziffer" der Zahl im Zauberersystem, ein „A". Dieses Gruppieren und Austauschen wird solange fortgesetzt, bis keine 36er-Gruppen mehr gebildet werden können und somit keine Plättchen mehr ausgetauscht werden können. Alles in allem ist das Umwandeln von Muggel- in Zaubererzahlen also nur ein Auflösen der 10er-Gruppierungen, die das Muggelsystem ausmachen, mit anschließendem Bilden der für das Zauberersystem grundlegenden 36er-Gruppierung. Kurz und knapp und dafür auch nicht ganz vollständig, begründete dieses Verfahren auch WallaceW aus ???. Aber vielleicht hilft dies all denen, die so und so abschalten, wenn eine Erklärung etwas zu lang wird:   Also, der Weg vom Muggelsystem ins Zaubersystem führt zum Erfolg, weil . . . die Basis des Zaubersystems B = 36 ist [(und durch diese Zahl wird ja immer dividiert), deswegen (und weil das Zaubersystem ein stellenbasierendes Zahlensystem ist,) ist auch die, eine Stelle linkstehendere Ziffer, 36 mal so viel wert, wie die gleiche Ziffer, die eine Stelle weiter rechts steht.]   Kaba aus ??? hat mir eine sehr schön anschauliche Lösung gesendet. Die Anzahl der Legotüten stimmt nicht immer ganz, aber das liegt daran, dass wohl kaum Platz für mehrere tausend Tüten ist. Denkt euch einfach Pünktchen. Sonst kann man hier das Bündeln oder Tauschen sehr schön nachvollziehen finde ich. Damit die Lösungsseite noch in angemessener Zeit von eurem Browser gelesen werden kann, sind hier nur Bilder mit geringer Auflösung. Wenn ihr auf die Bilder klickt, bekommt ihr die sehenswerte Lösung in besserer Qualität. Gleich beide Richtungen in einem wollte Perle86 aus Gryffindor erschlagen. Auch hier ist nicht alles ganz vollständig, aber ansonsten sieht man schön den Zusammenhang zwischen beiden Verfahren. Und wenn auch in vielen Argumentationen ein kleiner Teil fehlt, so finden wir doch in der Summe aller eurer eingesendeten Begründungen die wichtigsten Argumentationen wieder:   3. Bei dem Rechnen mit dem zaubersysthem ist es fast genau so wie bei dem Muggel Systhem. Nur das hier die Zehner potenzen Durch 36er potenzen ersetzt werden. Hat man im Mu 10 Rote Plättchen so erhält man ein blaues Hat man 10 Blaue Plattchen erhält man ein gelbes und so wieter. Hat Man im Za 36 rote Plättschen so erhält man ein blaues und hat man 36 blaue Plättchen so erhalt man ein Gelbes und so wieter. Im gegensatz dazu Funktioniert es beim zurück tauschen genau so. Für ein Gelbes Plättchen erhält man entweder 36 Blaue oder 1296 rote Plättchen (man beachte hier das jedes Blaue Plättchen einen wert von 36 roten Plättchen hat).